Zusammengesetzte Körper – online lernen
Du kennst aus deinem Umfeld bestimmt sehr viele zusammengesetzte Körper. Türme mit Dächern sind ein gutes Beispiel. Diese bestehen aus einem Zylinder und einem aufgesetzten Kreiskegel. Hier lernst du, was du bei den Berechnungen beachten musst, es gibt immer wieder kleine Fallen!
Berechnungen an zusammengesetzten Koerpern
Bei zusammengesetzten Körpern muss man besonderes Augenmerk darauflegen, welche Körper den Gesamtkörper ergeben.
Das Volumen des zusammengesetzten Körpers ergibt sich aus der Summe der Volumina der Teilkörper.
Nicht so bei der Oberfläche des zusammengesetzten Körpers, weil Flächen, die zur Oberfläche der Teilkörper gehören, nicht unbedingt zur Oberfläche des zusammengesetzten Körpers beitragen (siehe im Beispiel die Grundfläche des Kegels).
Beispiel: Der zusammengesetzte Körper oben besteht aus einem Zylinder mit aufgesetztem Kegel.

Für das Gesamtvolumen gilt:
- Vges = VZyl + VKe
Für die Gesamtoberfläche gilt:
- Oges = GZyl + MZyl + GKe + MKe = MZyl + OKe
Zusammengesetze Körper 03_1
Schwierigkeitsgrad 1
Arbeitsblatt-Nr. 12434
| Körper Zusammengesetze Körper | Schwierigkeitsgrad 1 Serie 3 |
Aufgabe 1
Ein quaderförmiges Haus hat eine Grundfläche von
| Modell 1 (Dach als Trapezprisma): | Modell 2 (Dach als Dreiecksprisma): |
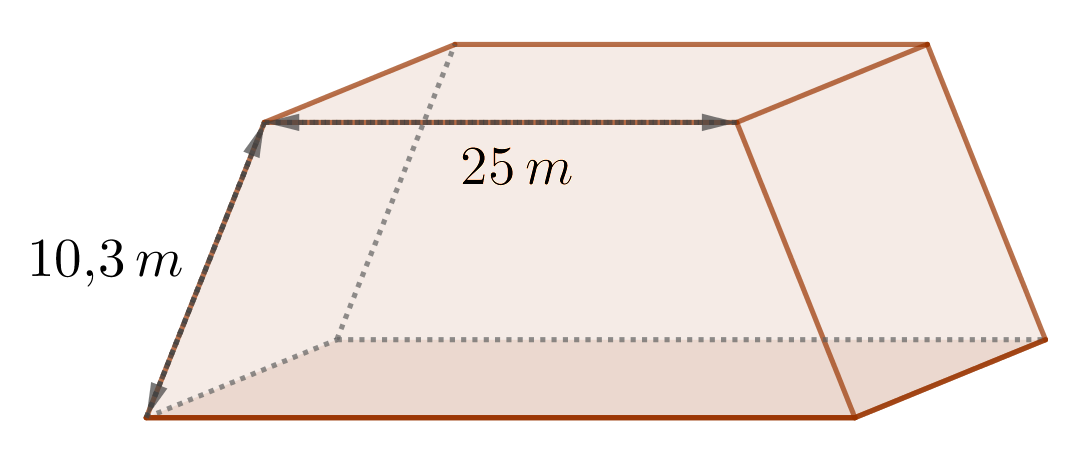 | 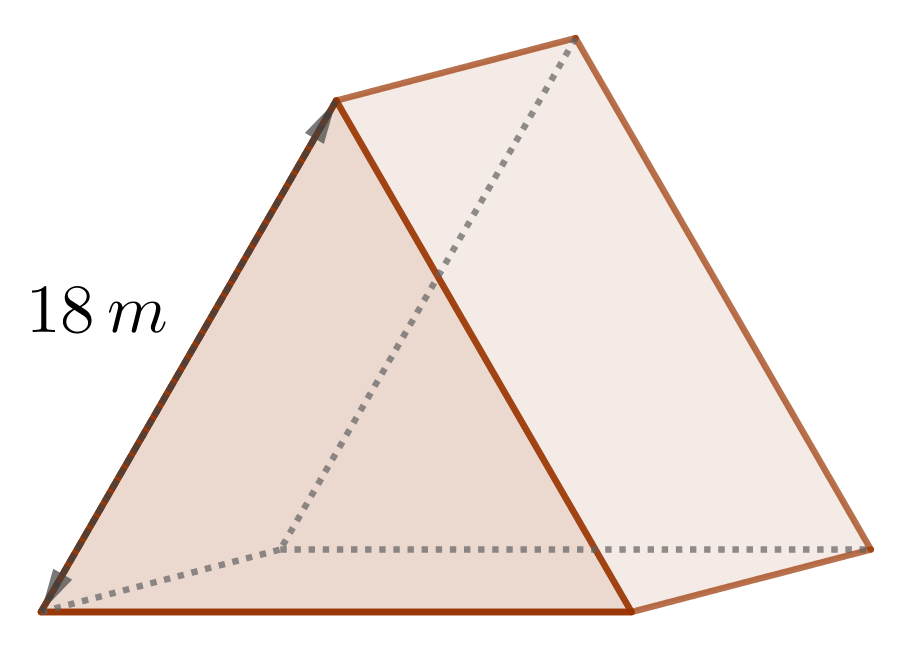 |
Berechne für jedes der zwei Modelle (die längere Seite des Hauses ist jeweils vorne abgebildet) die Oberfläche und das Volumen von Haus und Dach zusammen. Beachte, dass für die Oberfläche die Grundfläche des Hauses nicht dazugerechnet werden soll.
Aufgabe 2
Gegeben sind verschiedene Prismen, die die abgebildeten Figuren als Grundfläche besitzen. Diese bestehen aus regelmäßigen Teilfiguren. Berechne damit das Volumen dieser Prismen, wenn die Höhe jeweils
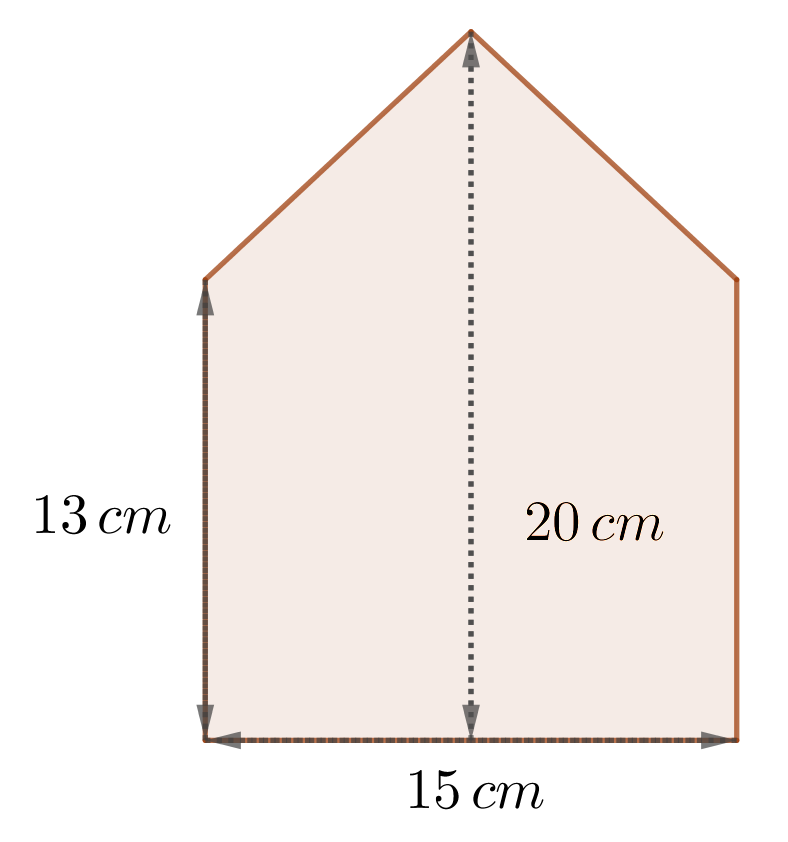 | 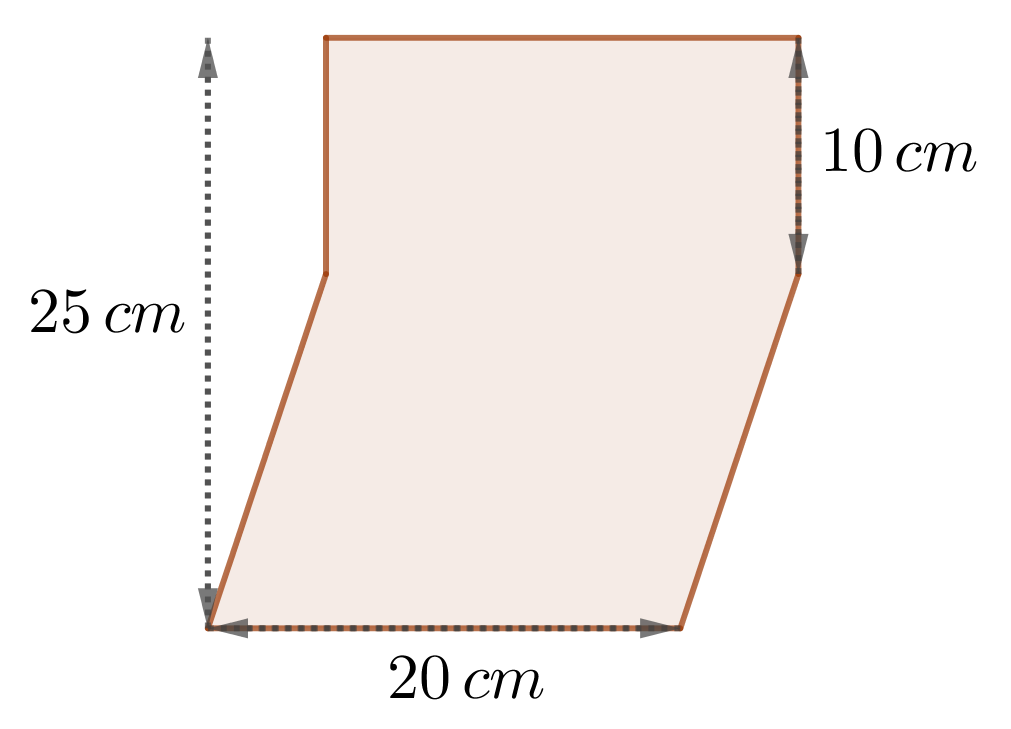 | 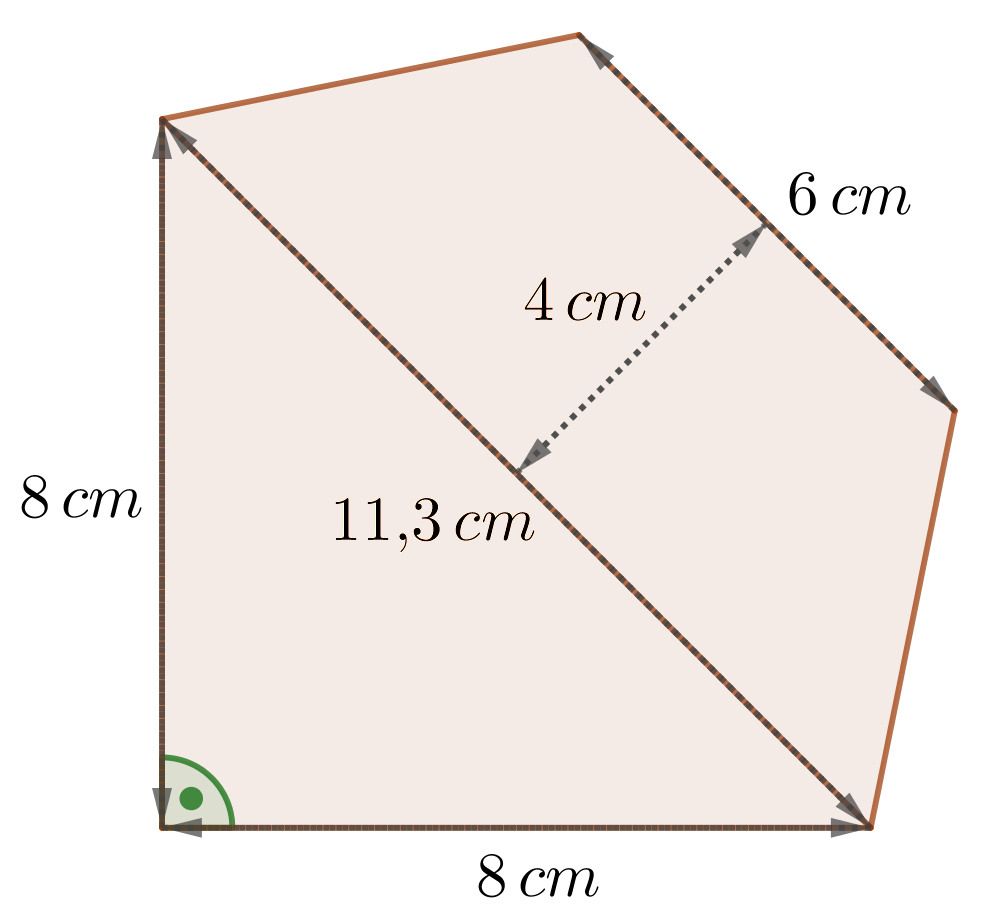 |
| Figur A: | Figur B: | Figur C: |
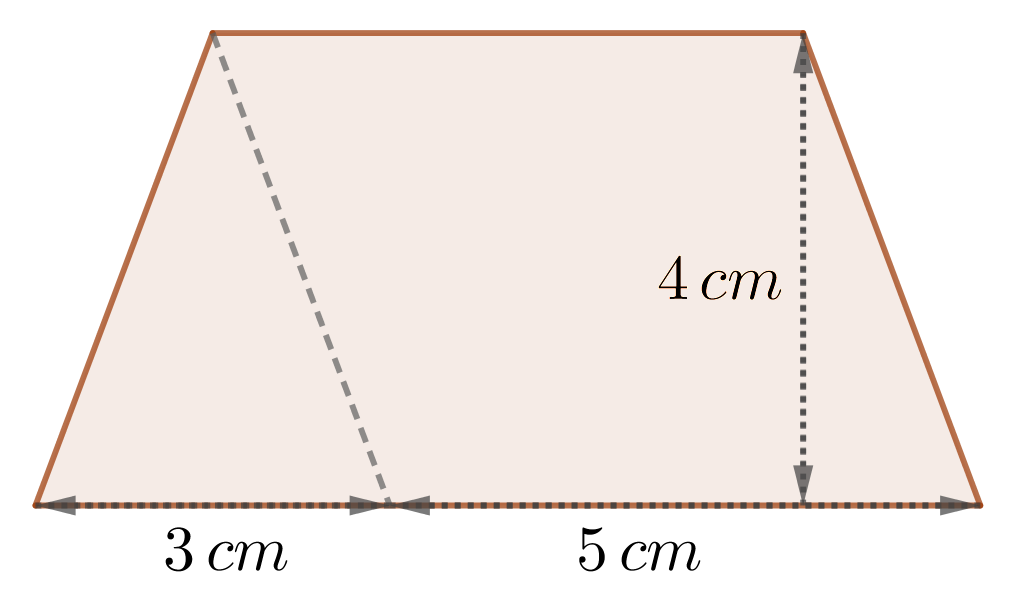 | ||
| Figur D: |
Zusammengesetzte Körper 02_1
Schwierigkeitsgrad 1
Arbeitsblatt-Nr. 12393
Schwierigkeitsgrad 1
Arbeitsblatt-Nr. 10813
Schwierigkeitsgrad 1
Arbeitsblatt-Nr. 799
Schwierigkeitsgrad 1
Arbeitsblatt-Nr. 5676
Schwierigkeitsgrad 2
Arbeitsblatt-Nr. 12435
Schwierigkeitsgrad 2
Arbeitsblatt-Nr. 10814
Schwierigkeitsgrad 2
Arbeitsblatt-Nr. 5677
Schwierigkeitsgrad 2
Arbeitsblatt-Nr. 800
Schwierigkeitsgrad 3
Arbeitsblatt-Nr. 12436
Schwierigkeitsgrad 3
Arbeitsblatt-Nr. 10815
Schwierigkeitsgrad 3
Arbeitsblatt-Nr. 5678
Schwierigkeitsgrad 3
Arbeitsblatt-Nr. 801

